Since DNA data strings compress, they are observed not to be random (in the sense of Chaitin [1]), although they do not compress a great deal. With four DNA bases, we might expect 2 bits per character if DNA were random, but we do not expect DNA to be completely random. However, zip or the Unix Lempel-Ziv file compressor, for example, can typically compress DNA marginally if at all.
A popular information-theoretic DNA compression scheme recently devised by Milosavljevic and Jurka [2]has been used in many places in the literature [3,4,5,6,7] for the discovery of new genes by the compression of DNA. We note here some inefficiencies in the Milosavljevic and Jurka (MJ) coding scheme [2,7]and give some improvements to their scheme, some of which run in linear time and improve the MJ method slightly, and others which run more slowly (e.g. quadratic time) but offer more marked compression.
In their compression method, Milosavljevic and Jurka [2] apply an encoding of previously occurring runs. They use 5 different code-words: four being the DNA bases, A, C, G and T, and a fifth code-word, P, introducing a pointer to a previously occurring subsequence. They advocate a code-word of length log2 5 for each of these. They also advocate encoding a run by a code-word of length 2 ×log2 n, where n is the length of the entire sequence. This redundant code encodes the start of the sequence with a code-word of length log2 n and likewise encodes the end of the sequence with a code-word of length log2 n .
We also note the slight difference between Milosavljevic and Jurka [2]and Milosavljevic [7], the latter of which compares two sequences by using one as the ``source'' and one as the ``destination''. As Milosavljevic [7,p41]points out, ``the only difference between the two algorithms is that in the former pointers point to the occurrences of words within the same sequence while in the latter they point to the occurrences of words within the source sequence.''.
Typical examples of non-randomness in DNA include poly-A runs, (AT)*, G-C rich regions, various common ``motifs'', ALUs and gene duplications. The ALUs are a family of sequences of about 300 base pairs, occurring many thousands of times in human DNA.
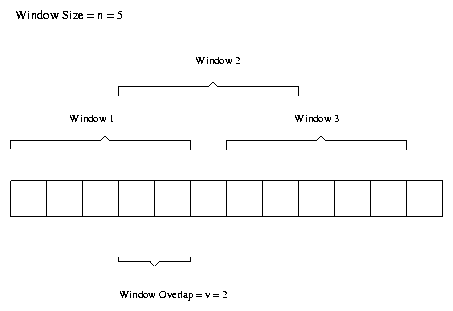
This method takes a DNA sequence and splits it up into windows of length fixed length n. These windows overlap by an amount v. Both n and v are parameters to the algorithm, with typical values [2] n = 128 and v = 64. Figure 1 is an example of this window size and overlap.

The Milosavljevic and Jurka method considers each window in turn independently of the rest of the sequence. Each window is encoded using 5 code-words one each for A, T, G, C and a pointer P used to encode a previously occurring subsequence. The code-word is fixed to be of length log25. Encoding a pointer consists of a pointer code-word, followed by a starting position of the previous run and a length of that run. The starting position and length are each encoded in log2n bits, where n is the size of the window.
Each window is encoded separately, and if this encoding is better than the null encoding (log24 = 2 bits per base) by a fixed threshold, then the window is deemed to be significant. This threshold is also a parameter to the algorithm.
The compression algorithms are illustrated using the complete DNA sequence of Human Tissue Plasminogen Activator Gene, GenBank accession number K03021, containing 36594 bases, as originally used by Milosavljevic and Jurka [2].
Since we did not have access to their source code, it was necessary to re-implement the MJ algorithm so that we could compare the results of their algorithm with the results of our algorithm . However, the re-implementation gave slightly different results to those presented in [2]. The same model was used as Milosavljevic and Jurka. A sliding window scheme was considered with windows of width 128. Each successive window was placed 64 positions further on. Milosavljevic and Jurka use a threshold of 22 » 7 + log2(36594) bits. Any window encoded in fewer than 256-22 bits (256 = 128 ×log2 4 bits from the encoding of the null model for a window of 128) is considered significant 1.
| Window | MJ bit saving | MJR bit saving |
| 7105-7232 * | 41 | 39.9 |
| 7169-7296 | 41 | 39.9 |
| 16833-16960 * | 38 | 37.6 |
| 16897-17024 | 41 | 39.9 |
| 17089-17216 | 22 | 21.2 |
| 23873-24000 * | 38 | 37.3 |
| 24065-24192 * | 35 | 34.9 |
| 24129-24256 * | 45 | 44.2 |
| 24193-24320 * | 49 | 48.9 |
| 24257-24384 * | 56 | 55.8 |
| 24321-24448 | 56 | 55.9 |
| 24385-24512 * | 22 | 21.1 |
Table 1 presents a comparison of the reported results in [2]and those obtained by our re-implementation (MJR). These encodings are shown in bits less than the null model, which has 128 ×log2 4 = 256 bits for a window of 128 characters. Those entries with an asterisk indicate windows in which our re-implementation found a significant saving but which were not explicitly mentioned in [2]; we used their executable to obtain their bit savings. Of the asterisked entries, the first two were not reported but the others constitute one segment of length 640 (from 23873 to 24512) with a gap of 64 (24001 to 24064). The long segment is similar to the segment 23888 to 24458 discussed by Milosavljevic and Jurka.
All following results will be compared to our re-implementation, MJR, of the MJ algorithm.
The first inefficiency in the Milosavljevic and Jurka [2] scheme that we can correct without in any way slowing down the algorithm is to say that, if we are currently in the k'th position in the sequence, then we can encode a pointer to a repeated subsequence using log2 ((k-1)(n-k+1)) bits, whereas Milosavljevic and Jurka use log2( n2) bits. This follows because Milosavljevic and Jurka [2,p408]permit runs to start and end at any place, providing codewords of length log2 n for both start and finish, whereas we note that there are (k-1) different positions from which the sequence can commence and then, given that the sequence only requires (n-k+1) new characters, there are only (n-k+1) positions in which the copy string can end, meaning that we can encode a sequence pointed to from position k using approximately log2((k-1)(n-k+1)) bits. This suggests that an MJ pointer at an end, at position k = 1 or at position k = n-1 , will be inefficient by as much as log2 n bits, whereas a pointer in the middle, at position k = n/2 , will only be inefficient by 1 + 1 = 2 bits.
On average, assuming the distribution of pointers to be approximately
uniform between 1 and n,
suggesting the MJ code to be inefficient by, on average, approximately
n
å
k = 2
log2 ((k-1)(n-k+1)/(n2))
=
log2(e)
n
å
k = 2
loge((k-1)(n-k+1)/(n2))
»
log2(e)
ó
õ
1
0
loge(x(1-x)) dx
=
log2(e) (
ó
õ
1
0
loge(x) dx +
ó
õ
1
0
loge(1-x) dx )
=
log2(e) ((-1) + (-1)) = -2 log2(e)
2 log2(e) bits » 2.88 bits, or 2 nits (natural
bits), per pointer.
We also note that our correction is fast, being implementable in linear time; we refer to our method below as the efficient pointer method. Theoretical results [8]show that, given a uniform method of encoding the pointers in the MJ scheme, a linear-time greedy algorithm leads to a global optimum. Although a greedy algorithm is not guaranteed to lead to a global optimum for our correction (above) to the MJ scheme, a greedy algorithm does lead to a linear-time algorithm which improves the MJ scheme, arriving at better compression.
We compared the MJR (Section 3.1) with our efficient pointer method (Section 3.2). As expected, more windows were found to have a significant compression under the same threshold of 22 bits. Table 2 shows the bit savings over the same null model for both these methods.
| Window | MJR bit saving | Efficient pointer bit saving |
| 7105-7232 | 39.92 | 44.45 |
| 7169-7296 | 39.92 | 46.53 |
| 16833-16960 | 37.60 | 42.73 |
| 16897-17024 | 39.92 | 45.32 |
| 17025-17152 * | 16.70 | 22.11 |
| 17089-17216 # | 21.28 | 28.35 |
| 23873-24000 | 37.33 | 51.37 |
| 23937-24064 * | 18.75 | 33.53 |
| 24001-24128 * | 11.72 | 29.15 |
| 24065-24192 | 34.87 | 54.97 |
| 24129-24256 | 44.23 | 63.07 |
| 24193-24320 | 48.87 | 67.73 |
| 24257-24384 | 55.77 | 76.54 |
| 24321-24448 | 55.90 | 70.48 |
| 24385-24512 # | 21.14 | 33.36 |
Of these windows, 3 were not found (denoted by *) by the MJ executable and 5 were not found by MJR (denoted by * and #). Recall the long segment from 23888-24458 reported in [2]and our corresponding MJR segment of length 640 (from 23873 to 24512) with a gap of 64 (24001 to 24064). The application of more efficient pointers now identifies this whole segment without any gap; furthermore, all intervening windows have significant compression. Also, by discovering the window 17025 to 17152, the MJR segment from 16833 to 17024 has been extended to include 16897 to 17216, giving a segment of length 384 from 16833 to 17216.
When encoding with fixed-size pointers (i.e., MJ pointers), a greedy linear time approach to choosing the encoding is guaranteed to be optimal [8]. However, no such guarantee of optimality exists for the variable size efficient pointers described above. Thus, there are various ways to choose an encoding when using these more efficient pointers.
With our efficient pointers, two obvious approaches can be taken to find an encoding in linear time. Firstly, the encoding arrived at using the MJ algorithm was used, as in Section 3.1, with the pointers later replaced with their more efficient variation. This is guaranteed to give an encoding in fewer bits for any region with at least one pointer (otherwise it encodes in the same number of bits, namely nlog2(5) bits, where n is the length of the region).
The second practical possibility is to ignore MJ pointers and use our efficient pointers throughout the greedy algorithm. This will generally find a better encoding than the previous method. While it could conceivably be worse, in practice this method was never found to be so. For this greedy encoding, savings of typically 0-10 bits out of ~ 200 bits were observed over the above-mentioned method and no new significant windows were found. In the following we use this second greedy algorithm.
Neither of the above linear time techniques for finding an encoding with variable length pointers are guaranteed to find the optimal encoding. However, it is possible to find the optimal encoding with variable length pointers, retaining a uniform prior on the starting position, in O(n2) time. This relies on the fact that the optimal encoding of a suffix of a string s[i..|s|] is independent of s[1..i]. So, to find the optimal encoding for s[i..|s|], all possible encodings are looked at, not just the one using the longest match starting at s[i] as in done for the greedy approach.
For the above-mentioned data, there were only 5 windows for which the greedy approach did not find the optimal encoding. Using the optimal encoding on these windows typically saved only 0.1 bits out of ~ 200 bits.
An encoding can be represented by placing a `-' between each symbol, and replacing a pointer by the sequence it encodes. This representation makes it easy to see repeat regions. An encoding for the sequence TGTACGTACCGT might be T-G-T-A-C-GTAC-CGT. Note the two repeats in this example sequence.
As an example, the encoding of the window from 23937 to 24064 is shown in Figure 2 as produced by the MJR algorithm, the greedy encoding with efficient pointers, and the optimal encoding with efficient pointers respectively. This region was not found by the MJ algorithm, but was found by both the greedy and optimal encoding with efficient pointers methods. Note the more efficient encoding of our greedy efficient pointer method. Also, the first two encoded repeats illustrate the marginal improvement that our optimal encoding gives over our greedy encoding method.
(a) Representation of MJR encoding (encoded in 237.25 bits)
G-A-T-A-G-A-T-T-G-A-T-A-G-A-TGATAGATGATAG-G-T-GATAGATT-A-G-A-T-A-A-ATA
GATGATA-C-A-T-A-C-ATGATAGAT-A-G-A-T-GATAAATAGA-C-G-G-T-A-G-A-T-G-G-A-T
-G-A-C-A-G-A-T-A-G-A-C-AGATGATAGGTGATAGAT-A-G-A-T-G-A-
(b) Representation of greedy efficient pointer encoding (encoded in 216.37 bits)
G-A-T-A-G-A-T-T-GATAGAT-GATAGATGATAG-G-TGATAGAT-T-A-G-A-T-A-A-ATAGATGA
TA-C-A-T-A-C-ATGATAGAT-A-G-A-T-GATAAATAGA-C-G-G-T-A-G-A-T-G-G-A-T-G-A-
C-AGATAGA-C-AGATGATAGGTGATAGAT-AGATGA-
(c) Representation of optimal efficient pointer encoding (encoded in 216.29 bits)
G-A-T-A-G-A-T-T-GATAGA-TGATAGATGATAG-G-TGATAGAT-T-A-G-A-T-A-A-ATAGATGA
TA-C-A-T-A-C-ATGATAGAT-A-G-A-T-GATAAATAGA-C-G-G-T-A-G-A-T-G-G-A-T-G-A-
C-AGATAGA-C-AGATGATAGGTGATAGAT-AGATGA-
Another inefficiency in the MJ coding is the assumption that A, C, G, T and pointer code-word P all have equal length code-words. This could be modified so that these were each permitted to (adaptively) have different probabilities. The search for these 5 probabilities could be done iteratively, starting with all equal to 1/5 for example, re-estimating and then iterating until convergence.
We note that this could be further extended to permit a gradually increasing probability of the pointer. We can thus think of our message as an encoding of a string based on the alphabet A, C, G, T, P and an encoding of the strings pointed to. Rather than assume this to come from a 0th order Markov model, we could use a higher-order Hidden Markov Model or a Lempel-Ziv compressor. Of course, the more general the model, the slower the compression.
We can come up with a much more efficient encoding of the runs. We can do this by encoding the start position for each run as having code-length log(k-1), since we know that the run must begin at least one place to the left of the current position. Letting li be the length of a run pointed to (where we assume that li ³ 1 ), we model run length by a geometric distribution and use the information-theoretic (compression-related) Minimum Message Length principle [9,10] to estimate the geometric parameter, p.
Making these modifications will slow down the algorithm. However, it is almost guaranteed to improve the search.
None of the techniques described so far, attempt to compress the sequence as a whole. Compressing the entire sequence is desirable because the compression rate gives an indication of the redundancy (and therefore the information-content) of the sequence. All modifications described here will be on the second technique described in Section 3.4, call this technique MJE (MJ efficient pointers). We show a number of modifications to the MJE technique to compress entire sequences. In all instances the sequence is broken up into non-overlapping windows of length w (where w is parameter to the algorithm). How to best apply overlapping windows to the methods described below remains an open problem.
If a sequence were `compressed' by applying the MJE method to each window, the result would (in general) be longer than the input sequence. This stems from the fact that most windows have few pointers, yet the pointers are assigned a probability of 1/5 thus increasing the code length for each of A,T,G and C over 2 bits per base. As a first step to deal with this, we can use the following method. Each window is allowed to be a `Ptr' window, or a `noPtr' window. A Ptr window is encoded with the MJE technique, and the noPtr window is simply encoded using 2 bits per base.
The sequence is then encoded by stating for each window whether it is a Ptr or a noPtr window, followed by the encoded window. The encoding method (Ptr or noPtr) for each window is chosen by encoding using both methods, then using the one which results in the shorter encoding. The encoding of stating whether a window is a Ptr or a noPtr is done adaptively with probability (numWinPtr+1)/(totWin+2) where numWinPtr is the number of Ptr windows so far, and totWin is the total number of windows seen so far.
For the sequence HUMTPA this compression method resulted in an encoding 0.41% shorter than the input. While this is not significant, it is a first approach, and does actually perform compression . Table 3 shows the Ptr windows from using this compression technique for the HUMTPA sequence.
| Window | Encoded Length (in bits) |
| 7169 - 7296 | 215.33 |
| 16897 - 17024 | 216.73 |
| 17025 - 17152 | 239.38 |
| 23937 - 24064 | 221.94 |
| 24065 - 24192 | 206.09 |
| 24193 - 24320 | 193.26 |
| 24321 - 24448 | 186.61 |
The next method tried is the same as the one described in the previous section except for a modification to the probability of the five possible events A,T,G,C and pointer. The noPtr windows are now encoded using an adaptive probability estimate for each of the four bases. That is, the probability of a given base, X, is (numX+1)/(total+4) where numX is the number of times X has occurred so far, and total is the total number of bases seen.
The Ptr windows are encoded by first encoding with probability Pptr whether the next symbol is a pointer or one of A,T,G or C 2. Again Pptr is estimated adaptively by Pptr = (numPtrs+1)/(numPos+2), where numPtrs is the number of pointers used so far, and numPos is the number of possible positions for pointers. The counts, numX, total, numPtrs and numPos are updated after each window. For noPtr windows, numX and total only are updated. After a Ptr window, numX, total, numPtrs and numPos are all updated. A region of the window that has been encoded using a pointer (ie. it is a duplicate of something earlier in this window), does not contribute to the updating of any of these counts.
For the sequence HUMTPA this compression method resulted in an encoding 0.54% shorter than the input. The final probabilities were as follows: P(A) = 0.26, P(T) = 0.25, P(G) = 0.25 and P(C) = 0.24, which is very close to a uniform distribution of the bases. The final pointer probability was P(pointer) = 0.02 which is much less than 1/5, used in the earlier MJ techniques. The encoding of the HUMTPA sequence with this compression scheme resulted in 23 windows being encoded with the Ptr method. These are shown in Table 4.
| Window | Encoded Length (in bits) |
| 7169-7296 | 215.41 |
| 8961-9088 | 256.45 |
| 10497-10624 | 243.54 |
| 16001-16128 | 253.83 |
| 16897-17024 | 199.79 |
| 17025-17152 | 219.70 |
| 19073-19200 | 245.00 |
| 19841-19968 | 247.61 |
| 21249-21376 | 251.42 |
| 21505-21632 | 244.40 |
| 21633-21760 | 253.25 |
| 22529-22656 | 251.34 |
| 23809-23936 | 251.06 |
| 23937-24064 | 226.98 |
| 24065-24192 | 218.97 |
| 24193-24320 | 203.05 |
| 24321-24448 | 194.06 |
| 24449-24576 | 253.99 |
| 24961-25088 | 247.87 |
| 26369-26496 | 241.55 |
| 29057-29184 | 237.43 |
| 34433-34560 | 250.20 |
| 36481-36594 | 212.91 |
The overall compression achieved by the two previous methods is small. In an attempt to improve the overall compression, we now apply a fixed size Markov Model to estimate the probability of the bases A,T,G and C. Each Ptr window can be encoded using a Markov Model of order in the range 0 to maxOrder, so each Ptr window first encodes the order of the Markov Model used. This encoding of the order of the Markov Model used is done in log2(maxOrder+1) bits, assuming each order equally likely a priori. The order of the Markov Model used in Ptr windows was found to have little effect on the overall compression, however it did affect the number of windows encoded using the Ptr method varying from 6 to 9 windows for the HUMTPA sequence. This is because the encoding using the Ptr method is often close (in terms of bit length) to the encoding using the noPtr method - thus a small change in the Ptr encoding can affect whether a window is encoded using the Ptr or noPtr method.
We applied this compression technique to the HUMTPA sequence and set maxOrder = 5, and fixed the Markov Model for Ptr windows to be order 0. The compression achieved was 4.3%. Only 6 windows were encoded using the Ptr method, these windows are shown in Table 5. This large decrease in Ptr windows compared to the previous section is due to the noPtr windows being compressed by the Markov Model. Thus the Ptr windows are not the only `significant' windows, some of the windows encoded using the noPtr method compress well and thus should also be deemed significant. In the above example all but 62 of the 286 windows were encoded in fewer bits than the null model (256 bits); so exactly what is significant is difficult to quantify.
It is interesting to note for the HUMTPA sequence, the usage of the Markov Model order was approximately uniform over orders 1 to 5 with order 0 used only rarely.
| Window | Encoded Length (in bits) |
| 7169 - 7296 | 215.41 |
| 16897 - 17024 | 200.97 |
| 17025 - 17152 | 220.75 |
| 23809 - 23936 | 252.68 |
| 23937 - 24064 | 226.18 |
| 36481 - 36594 | 215.14 |
DNA sequences are compressible, so they are not random. But they are not highly compressible. It is therefore necessary for coding methods to be as efficient as possible. Inefficiencies in the coding method will lead to structure within the DNA being missed.
The Milosavljevic and Jurka method is popular for the discovery of DNA motifs and compression. We have demonstrated an inefficiency in their use of pointers. We have devised and implemented various linear and quadratic time schemes which, in better compressing the DNA, have extracted longer segments of biological interest. We recommend the use of our greedy encoding algorithm using our efficient pointers throughout, particularly for long sequences. We have also proposed some further theoretical extensions. We have also proposed several techniques for applying the Milosavljevic and Jurka method to compress an entire DNA sequence.
1The probability of any window having a short encoding would be guaranteed not to exceed 2-7 » 0.01.
2Note that this two part encoding is equivalent to rescaling the distribution of A,T,G,C to allow for another event of probability Pptr